z(b) = ![]() n-b
n-b
On a Zipf�s Law Extension
to Impact Factors
Ioan-Iovitz Popescu
iovitzu@gmail.com
http://www.geocities.com/iipopescu
Abstract. The Lavalette�s law is further promoted with empirical arguments from its original area of impact factors of scientific journals. Alike its famous precursory Zipf�s and Mandelbrot�s rank-frequency laws, the Lavalette�s law offers the promise of various applications also beyond its original meaning. Thus, an alternate reduced rank-frequency distribution is introduced by assigning equal ranks to the words with the same frequency. Also the fractal behavior of self-similarity of actual rank-frequency curves belonging to different scales is revealed.
1. Introduction to Zipfian laws
As it is well known, the Zipf's law is an empirical law set up for linguistics in the early 1930s by the Harvard linguistic professor George Kingsley Zipf (1902-1950). This heralded the power law q(n) µ 1/n, now commonly called Zipf's law, which states that the frequency q of occurrences of some event (such as of a word in a text sample) is inversely proportional to its rank n. As often happens, there are forerunners, as displayed in a time table of bibliometrics by Ronald Rousseau (2001). Actually, G. K. Zipf (1935, 1949) originally described a broad statistical regularity of natural languages and proposed two complementary empirical laws of word frequencies, as highlighted by Landini (2000), namely:
1. �The rank-frequency law. This is the most famous one; unfortunately many people call it "Zipf's law" as if it was the only one. � The procedure to estimate this relation is very simple: the words in a text are sorted by decreasing frequency and a rank number is assigned to each word. For words with the same frequency, the sub-sorting and ranking is arbitrary. The plot of log (frequency) versus log (rank) approximates a straight line of slope -1.�
2. �The number-frequency law. � The plot of log (frequency) versus log (number of words with the same frequency) approximates a straight line of slope -0.5. While the rank-frequency law tends to occur for the high frequency words (although not necessarily for the first few ranking positions), the number-frequency law is observed for the low frequency words.�
Let us first discuss the Zipf�s rank-frequency law as currently expressed by the more general power-law function
q(n) = c n�b
with the scaling constant c = q(1) and the exponent b close to unity (b = 1 in the original Zipf�s expression). In other words, the rank-frequency data should lay on a straight line with slope -b when plotted in a double-logarithmic log (n), log (q) graph. Generally, q(n) can be any quantity used in ordering a set of occurrences, such as the frequency of natural or randomly generated words, size of cities or other settlements, income size, frequency of access to web sites, size of oil and other mineral deposits, earthquake magnitudes, galactic intensities, up to genetic ranking for cancer classification. Indeed, there is an impressing list of natural and social phenomena revealing a Zipf�s power-law behavior (Li, 2003). However, the explanation, modeling and meaning of this mysterious law represents a permanent intellectual and interdisciplinary challenge from Zipf �s times up to the present days (Laherrère, 1996, 1998; Landini, 1997, 2000; Li, 1998, 2002; Manrubia, 1998; Marsili, 1998; Powers, 1998; Redner, 1998; Troll, 1998; Tsallis, 2000, Altmann, 2002; Debowski, 2002).
Alternately, the law can be expressed as well by the probability. Thus, defining the text length (L) by the total number of running words of the considered text, the ratio p(n) = q(n)/L represents the probability to find the word with rank n. For instance, in the English language, the probability of encountering the nth most common word is given roughly by p(n) = 0.1/n for n up to about 1000, or better by (Weisstein, 2003)
p(n) = 1/[n ln(1.78N)]
where N is the vocabulary size, i.e. the total number of different words of the given text. However, the simple hyperbolic Zipf�s law q = c/n cannot hold generally true and breaks down for less frequent words or when the vocabulary increases indefinitely since the harmonic series diverges. Indeed, we have the constraint that the probabilities p(n) = q(n)/L must sum to 1, inasmuch as the frequencies q(n) sum to L. From here it results the above divergence assertion, since summing over this probability distribution gives a non-convergent series. Therefore, faster converging probability distributions have to be used to model Zipf-like distributions in this limit, such as the Riemann zeta function, z, defined by the series
z(b) = ![]() n-b
n-b
One of the earliest extensions of the Zipf�s law, intended to account for the observed typical downward deviation of the higher-ranked words, has been performed by Benoit Mandelbrot (1954). This well-known mathematician of fractals (a term coined by him in 1975) modified the original Zipf�s law q(n) = c/n in the form
q(n) = [(N + r)/(n + r)](1+e)
containing three adjustable empirical corrections to estimate, namely, a slight correction (already added above) to the power 1, which became the exponent (1+e), a number r added to the rank n, and the size N of the vocabulary of the considered text. All these three parameters N, r and e depend on the text length and, for very large texts, 0 <e << 1 and 0 < r < 10 (Debowski, 2002).
The interest in the Zipf�s law formulation has also been rejuvenated by Laherrere (1996, 1998), Redner (1998), Tsallis (2000) and others. Thus, the main results of the studies addressed to citations of publications (Redner), or to citations of authors (Laherrere) were that the stretched exponential
q(n) µ exp[-(n/n0)b]
fits reasonably well the data for relatively small n-values. However, the needed asymptotic behavior to fit actual data is the inverse power law q(n) = c n�b with b = 3, a shape which can not be provided by the exponential. Better results have recently been obtained (Tsallis and de Albuquerque) with a function of the power-law type, namely
q(n) µ [1 + (b -1)-1ln]-b
with the exponent b = 2.89 close to the previous one.
2. The Lavalette�s law
In the following we will be concerned with Lavalette�s extension of the Zipf�s law and its excellent fitting with actual data of journal impact factors. This is a new ranking power-law established by the French biophysicist Daniel Lavalette (1996), barely more complex than the Zipf�s law, q(n) = c n�b. Actually, the role of n as independent variable is taken by the ratio n/(N - n + 1) between the descending and the ascending ranking numbers. Finally, Lavalette�s law states that the impact factor q (in the role of frequency) of a set of N scientific journals, ordered by the descending ranking number n, obeys the relationship
q(n) = c [Nn/(N - n + 1)]�b
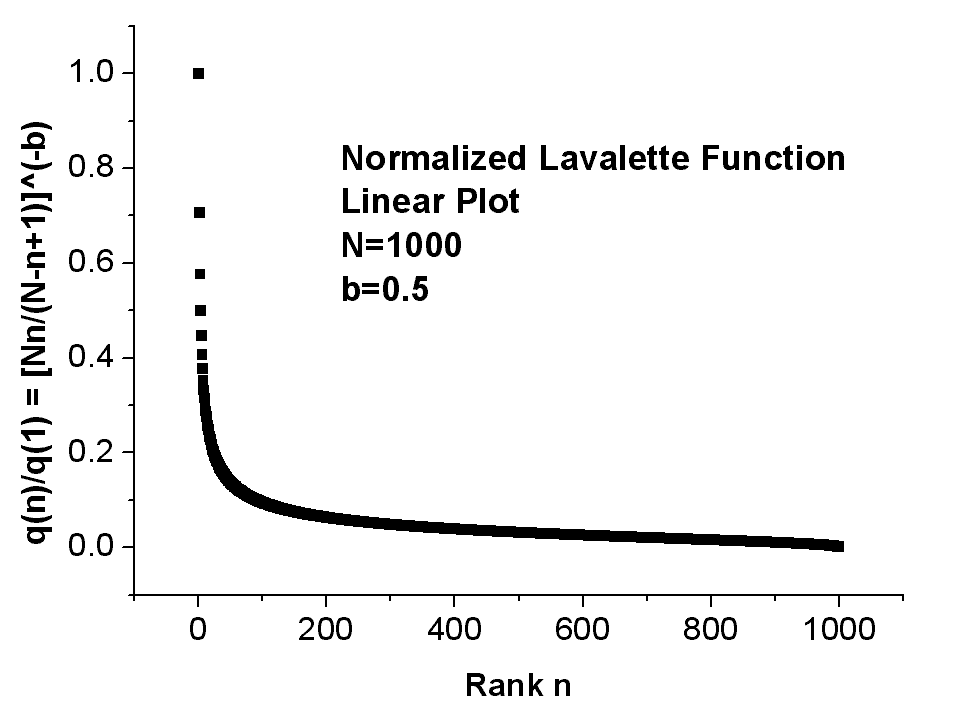
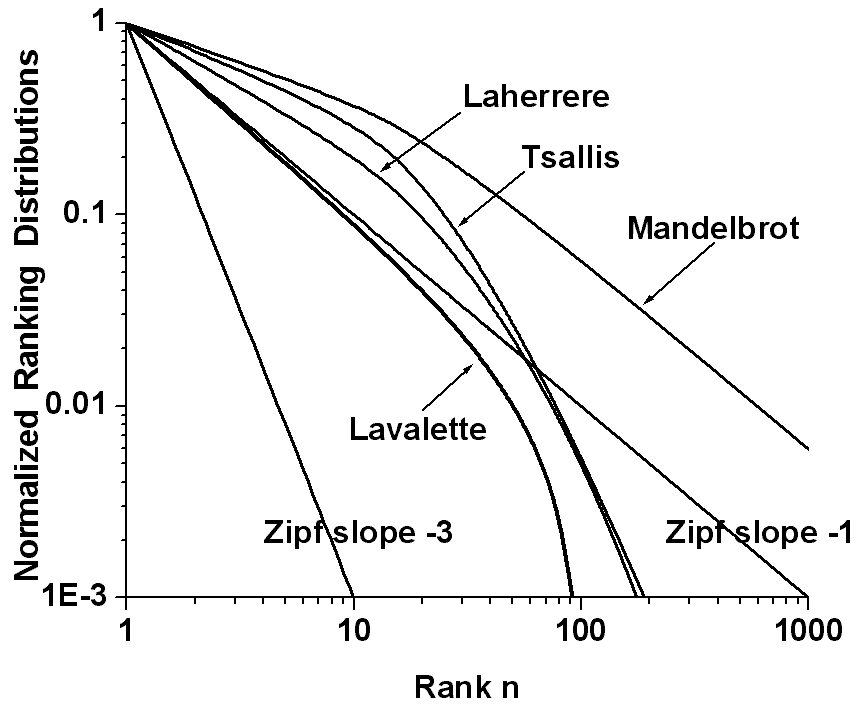
with two fitting parameters, namely the exponent b and the scaling constant c = q(1). Fig.1 shows the normalized Lavalette function q(n)/q(1) = [Nn/(N - n + 1)]�b as represented by three different plots, namely linear (top), semi-logarithmic (middle), and double-logarithmic (bottom). Perhaps the linear plot could be confused with a Zipf�s curve, but the semi-logarithmic graph follows a characteristic sigmoidal S-shape which by no means can be provided by the Zipf�s law. Also striking appears in a double-logarithmic diagram the downwards deviation from the Zipf�s straight line at higher-ranked words. Obviously, when viewed on a log [Nn/(N - n + 1)], log(q) plot the relationship is linear with slope �b and precisely this property allowed Lavalette to guess and test his law. Fig.2 schematically summarizes the essential features of the competing distributions presented above: Zipf�s, Mandelbrot�s, Laherrere�s, Tsalis�s, and Lavalette�s distribution. Note that also log-normal functions naturally bend in a convex form in a double-logarithmic plot.
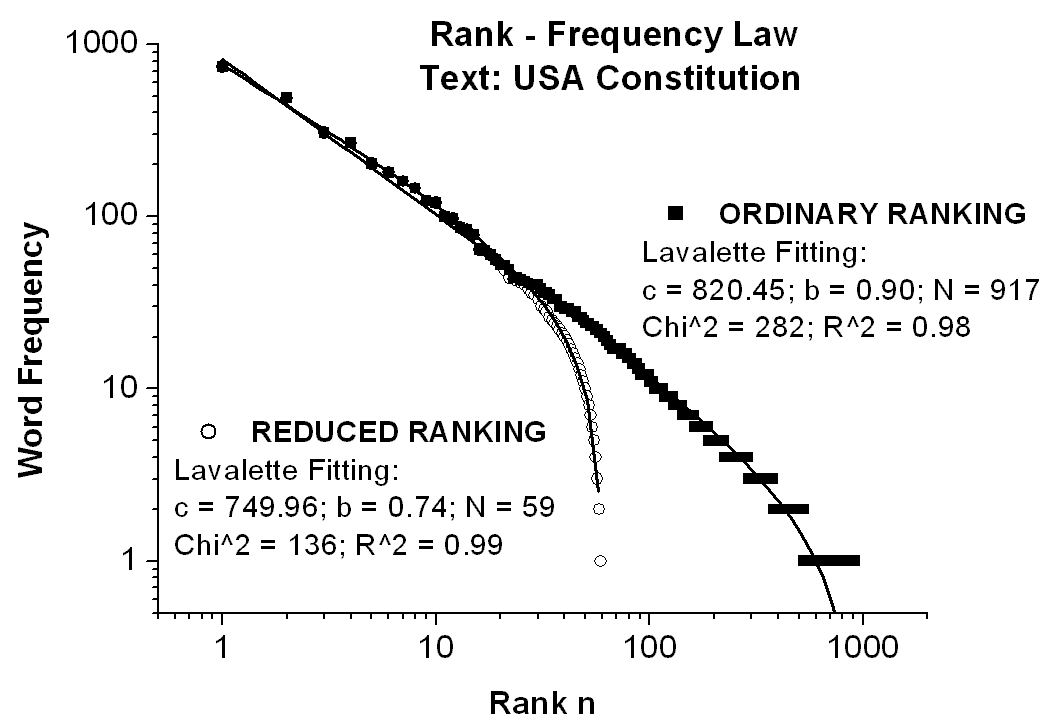
Actually, empirical Zipf curves follow only roughly a straight line with slope �b on a double-logarithmic graph, excepting the words of the low end (with highest ranks) when the actual data drop off quite steeply. Also the frequency of the most frequent words (with lowest ranks) do not necessarily follow as fast as expected by the original Zipf's law, that is proportional to 1, 1/2, 1/3, 1/4, and so on. A typical double-logarithmic rank-frequency plot and its Lavalette fitting for 917 distinct words (i.e. vocabulary) out of 7404 running words (i.e. text length), occurring in the text of USA Constitution, are given in Fig.3. For this purpose it will be instructive to discriminate between two possible rules concerning the ranks, namely allotting the ranks either distinctly or equally to the words with the same frequency. Consequently, we have to consider two types of rank-frequency distributions as illustrated in Fig.3, that is:
1. The ordinary rank-frequency distribution (upper curve in Fig.3) by assigning distinct ranks to the words with the same frequency (ranking within frequencies being otherwise arbitrary, e.g. alphabetical). In a double-logarithmic scale this leads to a slight convex bending and broadening towards the low end of the ranking distribution, a shape that is characteristic for any text and contributed much to the illusion of a general linear decrease. Though the deviation from the Zipf's law for the higher-ranked words is still a matter of controversy (Li, 1998), the convex bending is, however, almost always manifest, as we highlighted also in this case with the help of a Lavalette fitting. As usual, the meaning of N in the ordinary distribution is the total number of different words (the vocabulary).
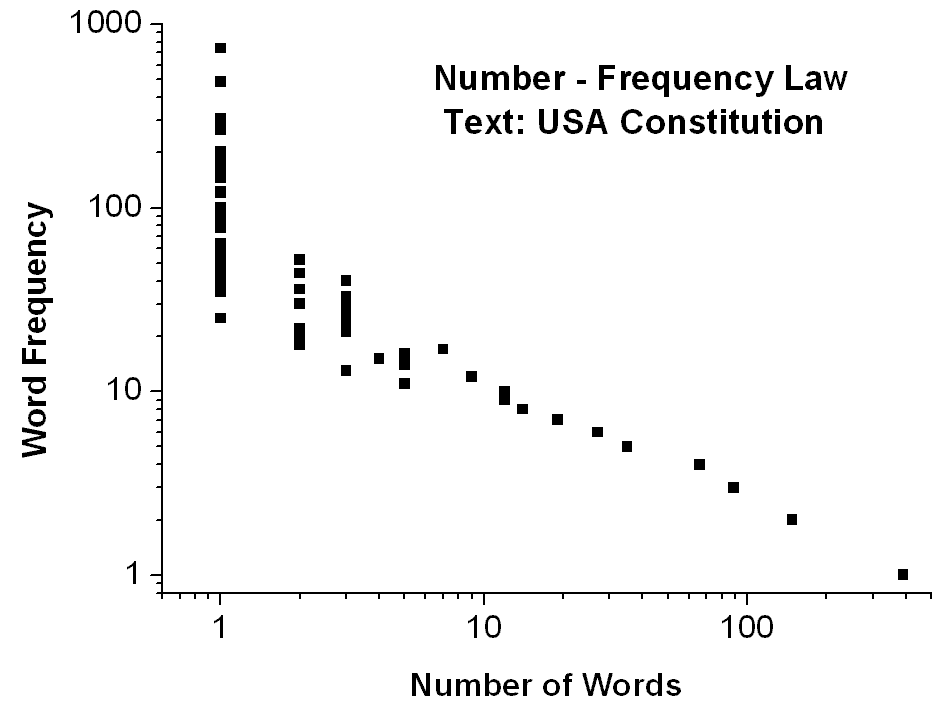
2. The reduced rank-frequency distribution (lower curve in Fig.3) by assigning equal ranks to the words with the same frequency. Obviously, the result of this rank rearrangement is a pronounced downwards bending of the ranking distribution, yet very well fitted by a Lavalette function. Also N means in this new remodeled ranking the total number of different frequencies occurring in the vocabulary spectrum when sorted by counts. From now on the link to the complementary number-frequency Zipf�s law is straightforward and the result is shown in Fig.4 by a plot of log (frequency) versus log (number of words with the same frequency), approximating a straight line with negative slope.
3. Further arguments and conclusions
Returning to the rank-frequency law, we will apply the same analysis to the rank-impact law as originally proposed by Lavalette (1996). As already shown in Fig.3, the Lavalette fitting can be achieved with the help of a single two-parameter (b and c) function along the entire range of frequency count. If necessary, also N can be used as a third tuning parameter in order to complete the missing data and to fix the needed set size. Empirical arguments for Lavalette�s distribution were previously illustrated in an addendum on the Lavalette ranking law to the web-article �Science Journal Ranking by Average Impact Factors� (Popescu, 2002) for journals ranked by average impact factors and sorted by scientific fields, by title initial letters, or by uniform random sub-sorting. The main conclusion is that the Lavalette�s distribution appears the best suited to fit the impact factor data among all the competing functions of Fig.2. In the present article an updated impact factor database will be used, as gathered in the file Science_Journal_Ranking_in_2001_2002_2003(Popescu, 2003), for a further empirical plea over the Lavalette�s extension of the Zipf�s law. For this purpose, Fig.5 and Fig.6 illustrate the ordinary and the reduced rank-impact distributions and their Lavalette fitting for the average impact factors of a whole set of 8011 scientific journals, respectively of an arbitrary subset of 1018 scientific journals with given title initial (here the letter A by chance chosen). In this case N means the total number of journals for ordinary ranking and the total number of different frequencies for reduced ranking.
One may conclude that, perhaps the major feature of actual rank-frequency or rank-impact curves of various subsets is that these look the same on any scale, including the curve describing the whole set. The striking fractal behavior of functional self-similarity of Lavalette�s curves is non-trivial, as it is the case with Zipf�s straight lines, and again the name of Mandelbrot and of his fundamental books on fractals should be recalled (Mandelbrot, 1977, 1983; 1997). Self-similarity is clearly manifest in actual data whenever one compares the Lavalette distributions of subsets between them or with the whole set distribution, as proven by the pair of Fig.5 (whole set of 8011 journals) and Fig.6 (subset of 1018 journals having title initial letter A). Self-similarity is further illustrated in Fig.7 for the ordinary ranking curves of the whole set of 8011 SCIENCE journals and of three successive subsets of 609 PHYSICS journals, out of which 85 OPTICS journals, and out of which 44 journals containing the phoneme OPT in the title. Obviously, if the ordinary curves are self-similar, the reduced ones, not shown in this figure, are likewise. Notice that the initial coalescence of OPTICS and OPT curves is caused by the coincidence of the first few ranking positions. Also the self-similarity is rather approximate than perfect and the statistics gets poor and poor according as we magnify by successive sub-sorting. Generally, from a massive empirical evidence one may conclude that self-similar Lavalette�s rank-frequency or rank-impact distributions govern the ranking of any kind of sub-sorting. Moreover, alike its famous precursory Zipf�s and Mandelbrot�s laws, Lavalette�s law offers the promise of various applications also beyond its original meaning of merely citation frequency.
Acknowledgments. The author is highly grateful to Professors Gabriel Altmann, Daniel Lavalette, and Mircea Oncescu for their interest in this work. Hearty thanks are also due to Dr. Magdalena Nistor and Drd. Sorin Vizireanu for their valuable help in computers and homepage. Since my first stage in Germany as a Humboldt Dozentenstipendium fellow (October 1967 � March 1969), I am always pleased to acknowledge the Alexander von Humboldt-Foundation for generous donations and computer facilities.
Prof. Dr. Ioan-Iovitz
Popescu
Member of the Romanian Academy
Bucharest, June 23, 2003
References
Altmann G., Editor (2002) Glottometrics 3, 4, volumes dedicated "To Honor G. K. Zipf" at his 100th birthday anniversary, RAM-Verlag, Lüdenscheid, Germany, http://www.ram-verlag.de/
Debowski L. (2002) Zipf�s Law Against the Text Size: A Half-rational Model, Glottometrics 4 (submitted)
Laherrère J. (1996) �Parabolic fractal� distributions in Nature, C.R. Acad. Sciences, Ser. IIa, 322, n.7, 535-541
Laherrère J., Sornette D. (1990) Stretched exponential distributions in nature and economy: "fat tails" with characteristic scales, Eur. J. Phys. B, 2, 525-539
Landini G. (1997, 2000) Zipf's laws in the Voynich Manuscript, http://web.bham.ac.uk/G.Landini/evmt/zipf.htm
Lavalette D. (1996) Facteur d�impact: impartialité ou impuissance ?, Internal Report, INSERM U350, Institut Curie - Recherche, Bât. 112, Centre Universitaire, 91405 Orsay, France (November 1996), see URL http://www.curie.u-psud.fr/U350/
Li W. (1998) Comments on "Zipf's Law and the Structure and Evolution of Languages" by Tsonis A.A., Schultz C., Tsonis P.A., (1997) Complexity, 2(5), pp.12-13 (letter to the editor), Complexity, 3(5), pp.9-10, see URL http://linkage.rockefeller.edu/wli/pub/comp98_zipf.html
Li W. (2002) Zipf's Law in Importance of Genes for Cancer Classification Using Microarray Data, http://linkage.rockefeller.edu/wli/pub/
Li W.(2003), W Li's references on Zipf's Law, http://linkage.rockefeller.edu/wli/zipf/
Mandelbrot B. B. (1954) Structure formelle des textes et communication: deux etudes. (Formal structure of texts and communication: two studies) Word, 10, 1-27
Mandelbrot B. B. (1977, 1983) The Fractal Geometry of Nature, Freeman, San Francisco, section 38, Scaling and Power Laws without Geometry. For a comprehensive bibliography visit Math Archives at URL http://archives.math.utk.edu/topics/fractals.htmland the Spanky Fractal Database at URL http://spanky.triumf.ca/www/welcome1.html
Mandelbrot B. B. (1997) Fractals and Scaling in Finance: Discontinuity, Concentration, Risk, Springer Verlag
Manrubia S. C., Zanette D. H. (1998) Intermittency model for urban development, Phys. Rev. E, 58, 295
Marsili M., Zhang Y.-C. (1998) Interacting Individuals Leading to Zipf�s Law, Phys. Rev. Lett., 80, 2741
Popescu I.-Iovitz, Ganciu M., Penache M. C., Penache D (1997) On the Lavalette Ranking Law, Romanian Reports in Physics, 49, 3-27
Popescu I.-Iovitz (2002) Science Journal Ranking by Average Impact Factors, http://www.geocities.com/iipopescu/Jo_rankingb.htm ; Addendum on the Lavalette Ranking Law, http://www.geocities.com/iipopescu/Jo_rankingb.htm#references
Popescu I.-Iovitz (2003) Direct links to databases used for the graphs of the present article: http://www.geocities.com/iipopescu/USA_Constitution_Word_Frequency.xls(for Fig.3 and Fig.4) and Science_Journal_Ranking_in_2001_2002_2003 (for Fig.5, Fig.6, and Fig.7)
Powers D. M. W. (1998) Applications and Explanations of Zipf's Law, in New Methods in Language Processing and Computational Natural Language Learning, ACL, pp 152-160, http://www.uia.ac.be/conll98/pdf/151160po.pdf
Redner S. (1998) How popular is your paper ? An empirical study of the citation distribution, Eur. J. Phys. B, 4, 131-134
Rousseau R. (2001) Bibliometrics Timetable (Ronald Rousseau). For major links of interest in bibliometric research see the website http://apollo.iwt.uni-bielefeld.de/mw/bibliometrics/
Troll G., beim Graben P. (1998) Zipf�s law is not a consequence of the central limit theorem, Phys. Rev. E, 57, 1347
Tsallis C., de Albuquerque M. P. (2000) Are citations of scientific papers a case of nonextensivity ?, Eur. Phys. J. B, 13, 777-780, http://tsallis.cat.cbpf.br/biblio.htm
Weisstein E. W. (2003) Eric Weisstein�s World of Mathematics, Zipf�s Law, http://mathworld.wolfram.com/ZipfsLaw.html
Zipf G. K. (1935) The Psycho-biology of Language: An Introduction to Dynamic Philology. Houghton Mifflin Co, Boston, the first clear formulation of Zipf's law. George Miller (1965), a renowned linguist, summarized these studies in "Introduction" in Psycho-Biology of Languages by G. Zipf, MIT Press
Zipf G. K. (1949, 1965) Human Behavior and
the Principle of Least Effort: An Introduction to Human Ecology, Cambridge,
MA, Addison-Wesley (1949), 2nd edition, New York, Hafner (1965); a comprehensive
bibliography on Zipf's Law has been gathered by Wentian
Li from Rockefeller University, http://linkage.rockefeller.edu/wli/zipf/

|
|
Fig.1
A typical normalized Lavalette function q(n)/q(1) = [Nn/(N -
n
+
1)]�b
for N=1000 and b=0.5 in linear (top), semi-logarithmic (middle) and double-logarithmic
(bottom) plot.
|
 |
|
.Fig.2
Illustrating essential shapes of competing ranking distributions: Zipf�s,
andelbrot�s, Laherrere�s, Tsalis�s, and Lavalette�s (thicker) curve. Note
that also log-normal functions naturally bend in a convex form in a double-logarithmic
plot.
|
 |
|
Fig.3
Illustrating ordinary and reduced rank-frequency distributions and their
Lavalette fitting for the text of the USA Constitution, vocabulary size
= 917 words, text length = 7404 words. Notice the earlier higher-ranked
distribution bending of the reduced ranking as compared with the ordinary
ranking. N means total number of different words for the ordinary ranking
and total number of different frequencies for the reduced ranking.
The
corresponding excel list of words is attached (click here)
|
 |
|
.Fig.4
Illustrating the word number-frequency distribution for the text of the
USA Constitution, vocabulary size = 917 words, text length = 7404 words.
The
corresponding excel list of words is attached (click here)
|
 |
|
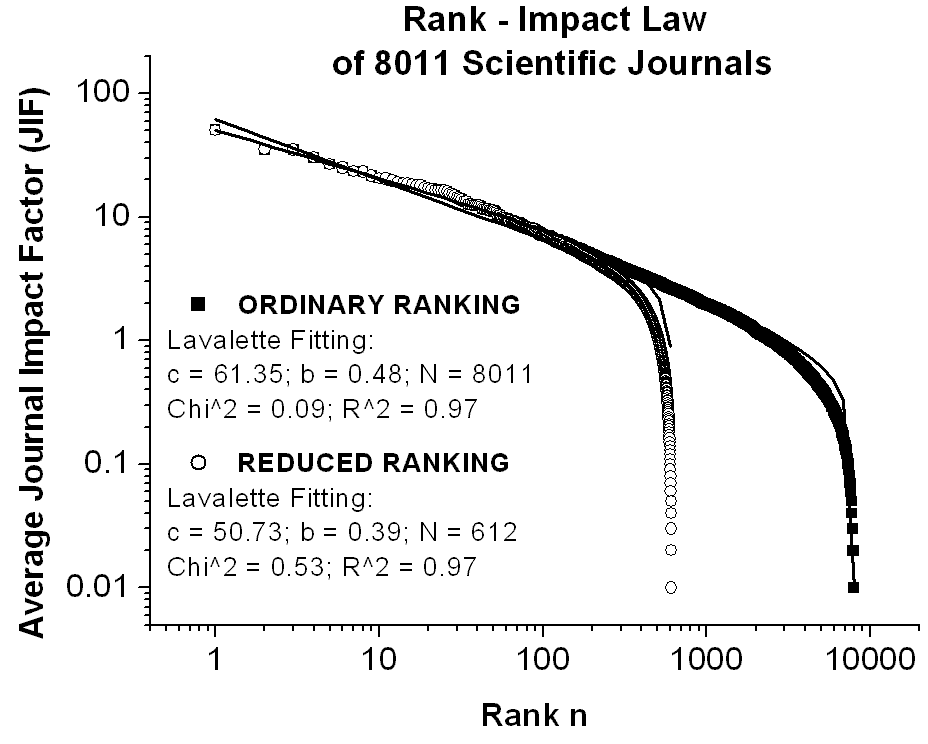
.Fig.5
Illustrating the ordinary and the reduced rank-impact distributions and
their Lavalette fitting for the average impact factors (JIF) of a set of
8011 scientific journals. Notice the self-similarity of the rank-impact
curves of Fig.5 and Fig.6. N means total
number of journals for the ordinary ranking and total number of different
frequencies for the reduced ranking. For a direct link to the used impact
factor database click here: Science_Journal_Ranking_in_2001_2002_2003
(214 KB), where JIF = average journal impact factor over all years of ISI
quotation (1974-2001) and ISI is the Institute for Scientific Information
(http://www.isinet.com).
|
 |
|
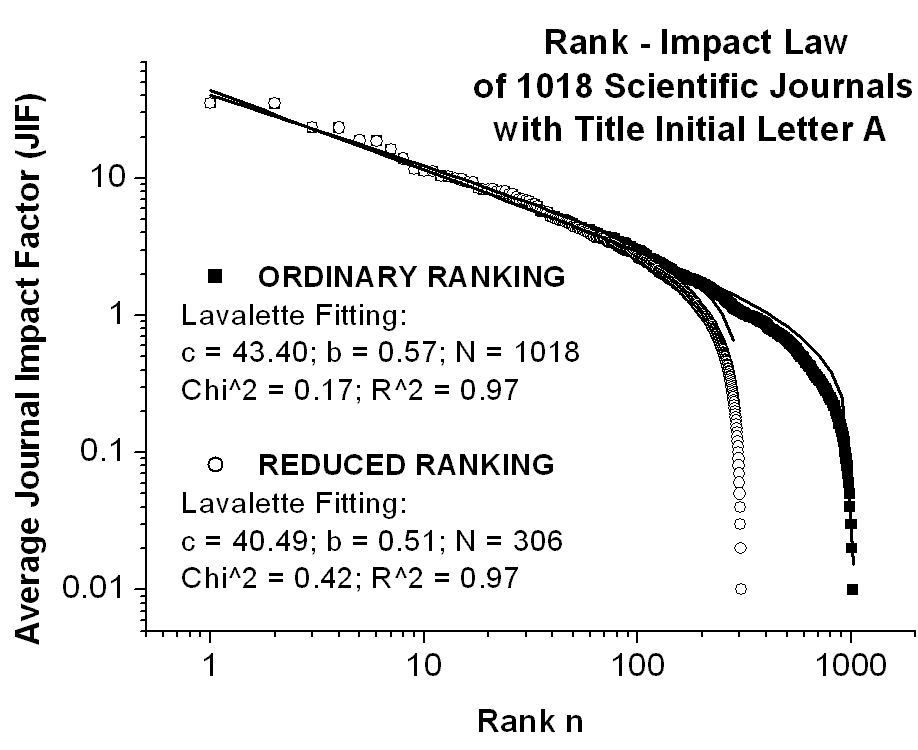
.Fig.6
Illustrating the ordinary and the reduced rank-impact distributions and
their Lavalette fitting for the average impact factors (JIF) of a subset
of 1018 scientific journals with the same title initial (here letter A),
out of a whole set of 8011. Notice the self-similarity of the rank-impact
curves of Fig.5 and Fig.6. N means total
number of journals for the ordinary ranking and total number of different
frequencies for the reduced ranking. For a direct link to the used impact
factor database click here: Science_Journal_Ranking_in_2001_2002_2003
(214 KB), where JIF = average journal impact factor over all years of ISI
quotation (1974-2001) and ISI is the Institute for Scientific Information
(http://www.isinet.com).
|
 |
|
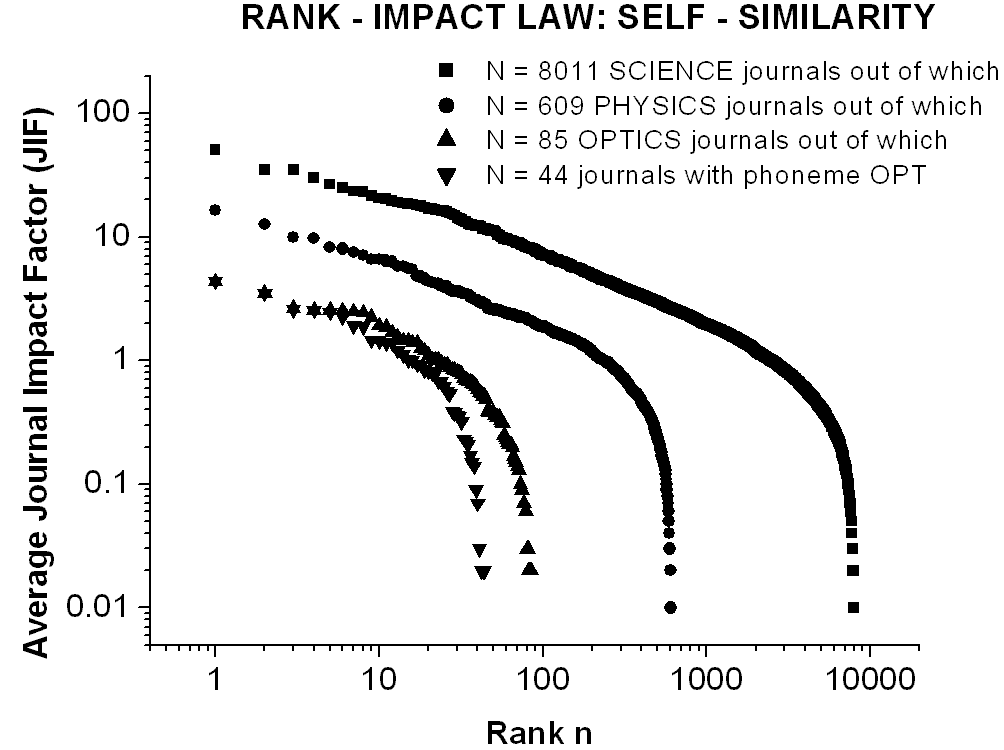
.Fig.7
Illustrating the self-similarity of ordinary rank-impact curves for the
average impact factors (JIF) of the whole set of 8011 SCIENCE journals
and of its three successive subsets of 609 PHYSICS journals, out of which
85 OPTICS journals, and out of which 44 journals containing the phoneme
OPT in the title. The reduced rank-impact curves, not shown in this figure,
are self-similar likewise. Obviously, the initial coalescence of OPTICS
and OPT curves is caused by the coincidence of the first few ranking positions.
For a direct link to the used impact factor database click here: Science_Journal_Ranking_in_2001_2002_2003
(214 KB), where JIF = average journal impact factor over all years of ISI
quotation (1974-2001) and ISI is the Institute for Scientific Information
(http://www.isinet.com).
|